서론
필자가 선형대수 관련 서적을 뒷부분부터 정리하기 시작했음으로 이보다 더 선행되는 개념들은 추후에 다루도록 한다.
요새 기술 블로그에 너무 손을 놔버려서 2학기 스터디에서 정리도 할겸 시작하게 되었다.
선형 방정식
방정식이란 변수가 포함된 식에서 해당 변수가 특정 값을 가질때만 성립되는 등식이다.
우리가 보통 학교 교육과정 내에서 선형 방정식을 떠올리게 되면 y = 2x + 1 이런 식을 떠올리게 된다.

보통 2개의 변수인데 x의 차수가 높아봤자 x^4 이거나 하다. 허나 선형방정식에서는 여러 개의 변수를 가질 수 있다.
3X + 2Y + 7Z = 32 (X,Y,Z는 모두 변수이다.)
이런 형태를 가질 수 있다.
물론 이처럼 변수가 3개 이상으로 늘어나면 우리가 평소에 접하면 이차평면이 아닌 그 이상의 형태를 가지게 될 것이다.
그리고 크게 유의해야할 점은 선형 방정식에서는 변수끼리의 곱이나 제곱근을 포함하지 않는다.
상수와 변수 간의 곱은 가능하나 변수끼리의 곱은 불가하다.
우리는 두 선형 방정식 X + 2Y = 8과 -2X + 4Y = 8이 있을때 두 선형방정식의 교점 (2,3) 을 선형 시스템을 만족시키는 해라고 부른다.
첨가행렬
3X + 2Y + 7Z = 32
2X + 9Y +6Z = 12
10X + 12Y + 4Z = 7
4X + 5Y +8Z = 10

이러한 선형 시스템의 상수부분만 모아서 행렬 형태로 나타낸 것을 첨가 행렬이라고 한다.
이러한 첨가 행렬에 기본 행 연산을 이용하면 선형 시스템의 해를 쉽게 구할 수 있다.
기본 행 연산은 3가지의 연산 규칙이 있다.
- 한 행에 영이 아닌 상수를 모두 곱한다
- 두 행을 교환한다
- 한 행의 배수를 다른 행에 더한다
1번의 예시이다. 말그대로 단순하다.

2번의 예시이다. 1행과 2행을 교환하였다.

3번의 예시이다. 4행의 -1의 배수를 3행에 더하였다.

가우스 조르단 소거법
가우스 조르단 소거법을 설명은 첨가 행렬을 사용하면서 끝에 상수 부분은 배제하고 계산하는게 수월하기 때문에 3x4의 첨가 행렬을 사용해서 예시를 들겠다.
가우스 조르단 소거법은 가우스 행렬을 만들어 행렬 시스템을 간단하게 계단하는데에 의의가 있다.
여기서 가우스 행렬이란 각행의 첫 원소가 1이고 1 아래의 원소는 무조건 0인 행렬이다.
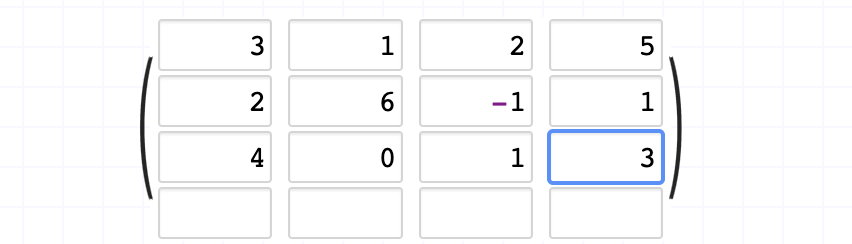
이러한 첨가행렬이 있다고 치자, 가장 오른쪽은 상수부분이다.
일단 첫번째 행의 첫 원소를 1로 만들기 위해 1/3를 곱한다.
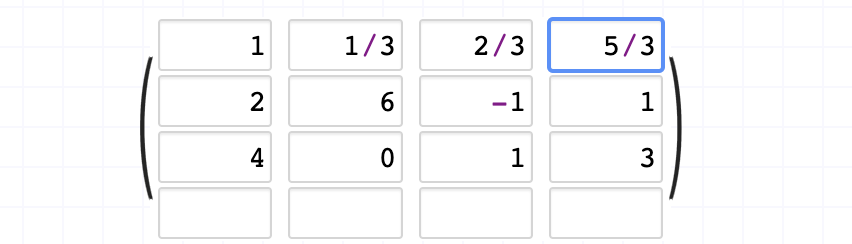
그다음 첫번째 행에 -2를 곱한 후 두번째 행에 더하는데 2행의 1열 원소를 0으로 만들기 위함이다.
첫번째 행에 첫 원소가 1이 되었으므로 바로 밑의 원소가 0이 되야하기 때문이다.
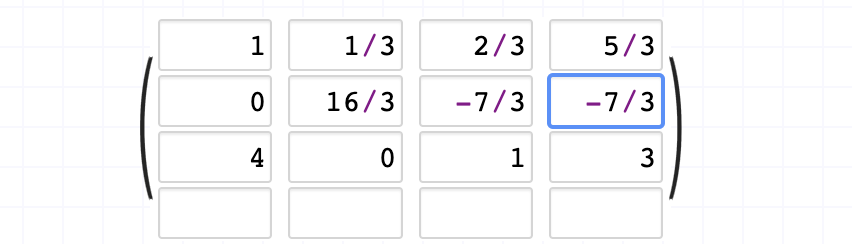
위와 마찬가지인 이유로 세번째 행의 첫번째 원소도 0으로 만들기 위해 첫번째 행에 -4를 곱한뒤 세번째 행에 더한다.

그 다음 두번째 행의 두번째 원소도 1로 바꾸어주기 위해 3/16을 두번째 행에 곱한다.

계산을 하다보니 3번째 행의 원소들이 분모로 3을 가지고 있어서 편의를 위해 3을 세번째 행에 곱해준다.

이후 세번째 행의 두번째 원소를 0으로 만들기 위해 두번째 행에 4를 곱한뒤 더해준다.

세번째 행의 세번째 원소를 1로 만들기 위해 -4/51을 곱해줍니다.
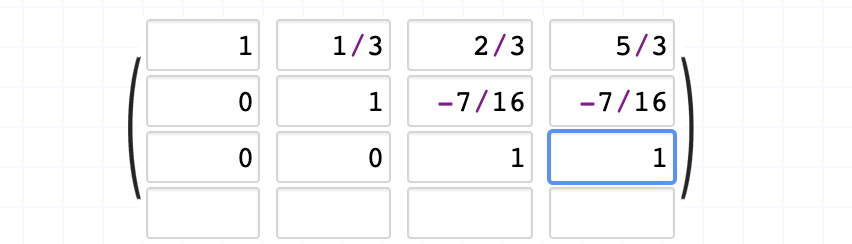
이 행렬을 다시 원래 식으로 되돌려주면
X + 1/3Y + 2/3Z = 5/3
Y - 7/16Z = -7/16
Z = 1
이렇게 정리가 가능하고 이제 우린 모든 변수를 다 구하였다.
물론 기약 가우스 행렬로 또 변환시켜서 더 편하게 대입없이 변수를 구할 수 도있다.
하지만 오늘은 여기까지